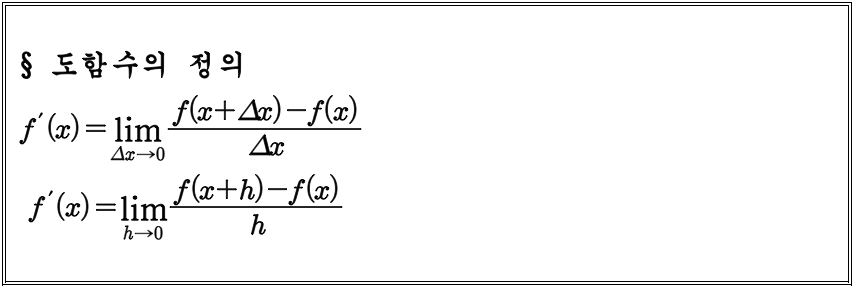#군포송정지구수학학원 #군포송정지구수학학원추천 #군포송정지구수학내신 #군포송정지구중고등수학추천 #송정지구수학내신 #송정지구중고등수학추천 #군포송정중고등수학학원추천 #의왕역수학원#의왕역중고등수학학원추천#의왕역중고등학교추천#의왕역중고등학교추천#의왕역중고등학교#부곡동구곡동구곡동구곡중학교#군포송정중학교추천#군포선종중고등학교내신�

안녕하세요. 의완역 중고등학교 수학추천 채움수학학원입니다.

오늘은 고등수학의 중요한 개념 중 하나인 “도함수와 미분”에 대해 알아보겠습니다. 이 개념은 미적분학에서 핵심적인 역할을 하며 다양한 현실 문제를 해결하는 데 활용됩니다.
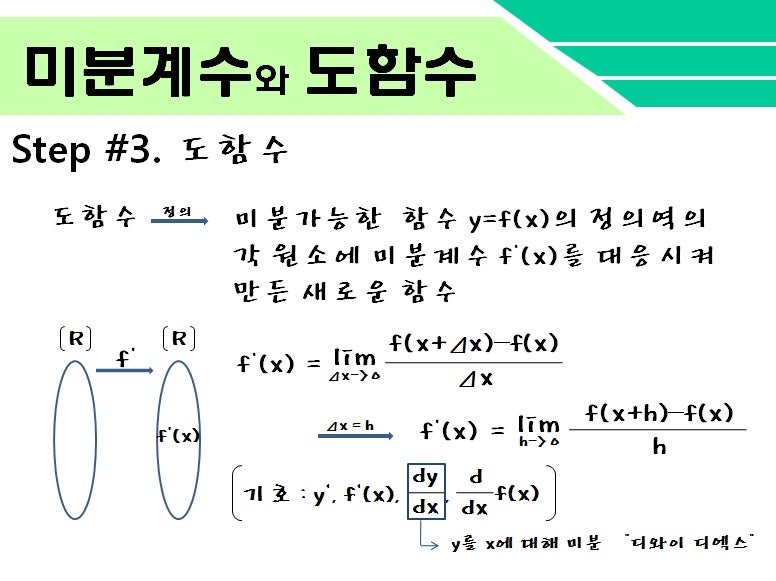
도함수와 미분의 시작도함수와 미분은 어떤 함수의 변화율을 나타내는 개념입니다. 함수는 어떤 입력값을 받아서 출력값을 내는 규칙이라고 생각됩니다. 그리고 이 함수의 변화율은 한순간의 작은 변화량에 대한 출력값의 변화를 의미합니다. 이것을 수학적으로 표현한 것이 ‘도함수’와 ‘미분’입니다.

미분이 정의된 함수 f(x)가 주어졌을 때, 이 함수의 도함수 f'(x)는 다음과 같이 정의됩니다.[ f'(x) = lim_{h to 0} frac{f(x+h)-f(x)}{h} 여기서 h는 매우 작은 변화량을 나타냅니다. 이는 입력값 x가 바뀔 때 그에 따른 출력값 변화를 나타냅니다.도함수의 해석 도함수는 어느 순간의 변화율을 나타내므로 어느 지점에서의 기울기를 의미합니다. 따라서 도함수의 값이 양이면 함수는 증가하고 음이면 함수는 감소합니다. 또한 도함수가 0이 되는 지점에서 함수의 최대 또는 극소치가 발생할 수 있습니다.
미분 응용 미분은 다양한 현실 문제에 적용됩니다. 가장 간단한 예로 속도와 위치의 관계를 생각할 수 있습니다. 어떤 물체의 위치 함수를 미분하면 그 물체의 속도를 알 수 있습니다. 이를 통해 다양한 물리적, 경제적 현상을 분석할 수 있습니다.채움수학학원, 미적분의 달인들이 모이는 곳! 지금까지 미적분의 기초인 도함수와 미분에 대해서 알아봤는데요. 앞으로 이런 흥미로운 수학을 깊이 학습하고 싶다면 채움수학학원을 추천합니다. 의왕역 중고등수학추천 채움수학학원은 수학전문학원으로 군포송정지구에 위치하고 있습니다. 수학만 일주일에 6시간씩 진행되며 학습성과를 체크하기 위한 테스트도 주기적으로 실시됩니다.

미통 과자에는 보충 학습이 제공되어 자신감을 키울 수 있습니다.

또한, 의왕역 중고등수학추천 채움수학학원은 중고등수학 전문으로 중등과 고등내신에 완벽하게 대비할 수 있는 커리큘럼을 제공합니다. 깨끗한 신축 건물과 강의실에서 진행되는 수업은 학생들에게 최고의 학습 환경을 제공합니다. 50m 네이버 더보기 / 오픈스트리트맵지도데이터x 네이버 / 오픈스트리트맵지도컨트롤러 범례부동산대로읍,면,동시,군,구시,도국

채움수학학원 경기도 군포시 송부로 82 더드림4차 4층 404호
채움수학학원 경기도 군포시 송부로 82 더드림4차 4층 404호

채움수학학원 경기도 군포시 송부로 82 더드림4차 4층 404호